Research Fields
We are a computational research group in soft condensed matter physics and computational physics. Our group focuses on investigating the behavior of matter at the nanoscale, utilizing state-of-the-art computational tools and techniques. Our researches include:
Phase transition and critical phenomena in complex substances
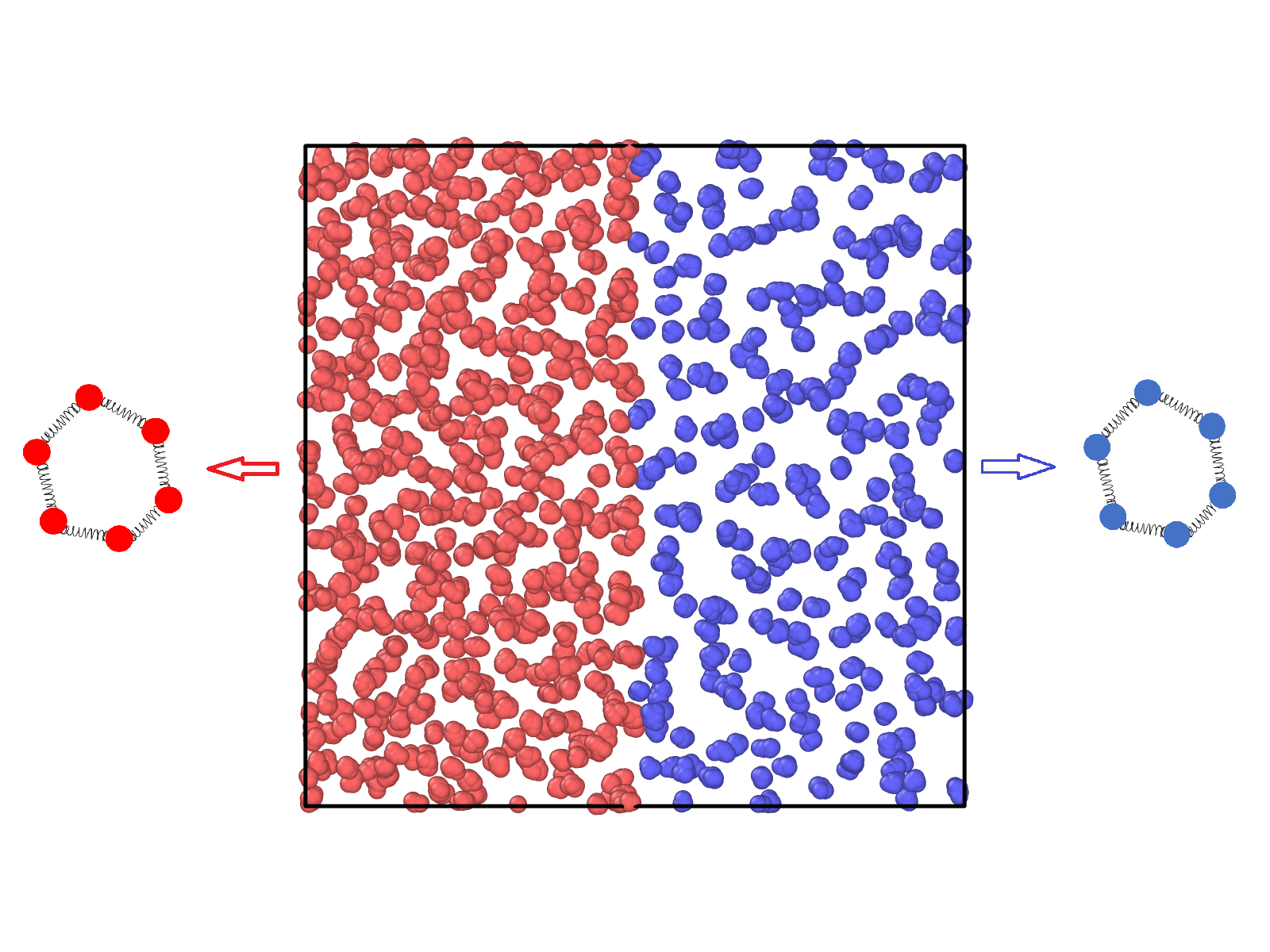
Phase transitions are common and important phenomena in nature[1]. For example, phase transitions between gas, liquid, and solid states can be well described by statistical physics, thermodynamics, and condensed matter physics. However, such theories do not apply to complex substances with liquid polymorphisms. Specifically, complex substances[2-3], such as water, silicon, sulfur, phosphorus, gallium, and hydrogen, exhibit anomalous properties in their liquid states. Despite having distinct electronic and molecular structures, these substances display similar anomalous properties in their liquid states, including structural, dynamic, and thermodynamic anomalies[4-6]. According to the liquid-liquid critical point scenario, single-component substances may exhibit a low-density liquid (LDL), a high-density liquid (HDL), and a transition between them (LLPT). The liquid-liquid critical point (LLCP) and the resulting critical fluctuation may be the source of the anomalous properties of complex liquids. The phase transitions in complex substances, such as LLPT, are intriguing and important phenomena. However, verification of the LLCP scenario is challenging because LLCPs are usually buried in the deeply supercooled region where crystallization occurs rapidly and is not easily accessible experimentally. How to trace LLPT and LLCP through easily detectable phase intervals has been at the forefront of this field.
References:
[1]X. Yu, R. Huang, H. Song, L. Xu, et al. Phys. Rev. Lett. 129, 210601 (2021)
[2]R. Li, G. Sun, L. Xu, et al. The Journal of Chemical Physics, 145, 054506 (2016)
[3]Z. Sun, D. Pan, L. Xu*, and E. G. Wang*, Proc. Natl. Acad. Sci. USA 109, 13177-13181 (2012)
[6]J. Luo, L. Xu*, E. Lascaris, H. E. Stanley, and S. V. Buldyrev, Phys. Rev. Lett. 112, 135701 (2014).
Interficial water structure and dynamics
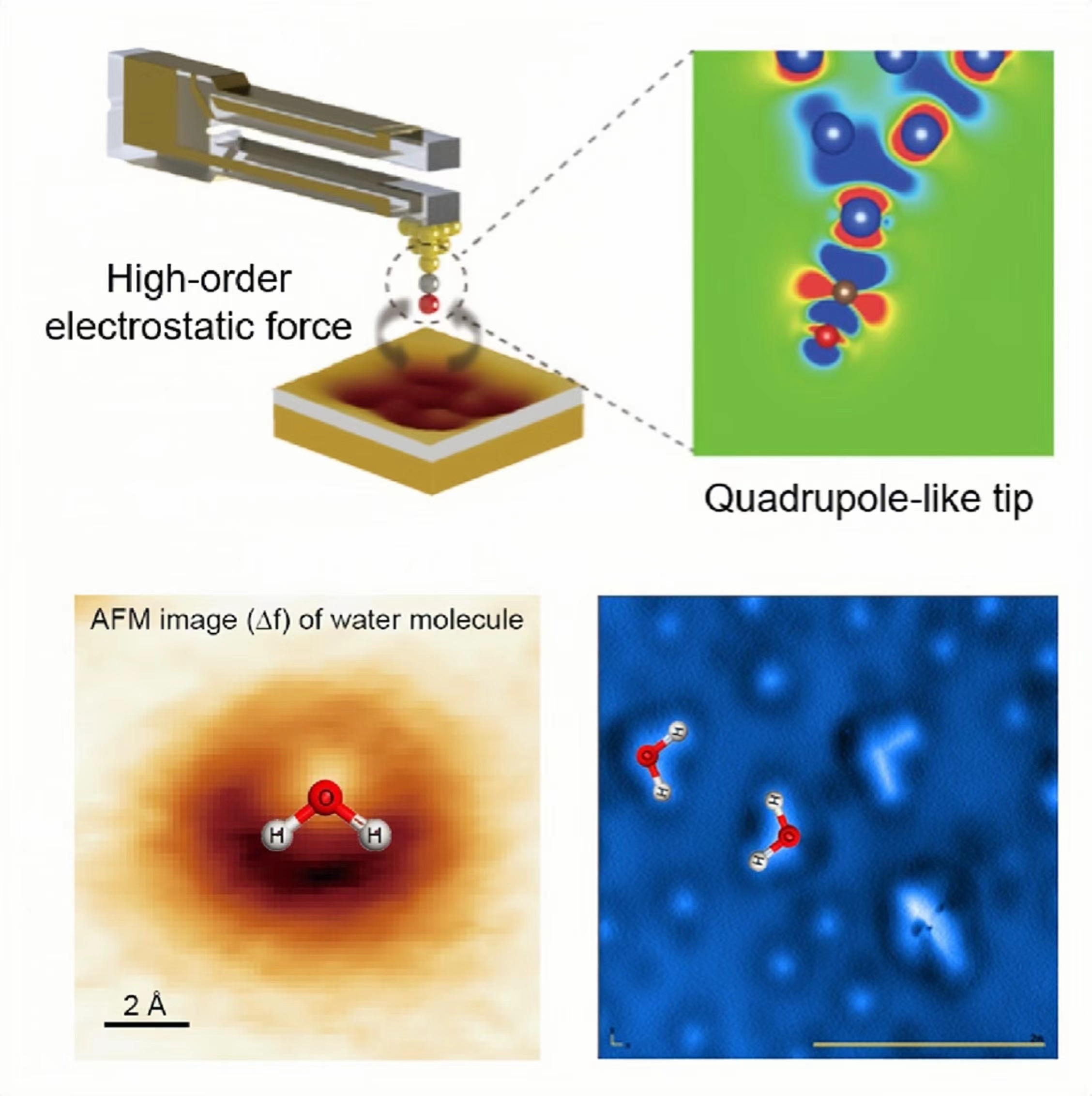
Interfacial water is essential in multiple scientific fields, including physics, chemistry, biology, energy, and materials science. Moreover, interfacial ionic hydrates are closely related to various essential issues in both applied fields and natural processes, including electrocatalytic processes, seawater desalination, biological ion channels, and chemical reactions. Understanding the atomic-level structure of different interfacial hydrogen bond networks, with or without ions, is crucial for elucidating the extraordinary properties exhibited by the water/solid interface in nature. With DFT calculations and AFM image simulations based on experimental data, we investigate the hydrogen bond network structures on various substrates[2-6], and analyze their physical and chemical characteristics, such as dynamic properties, proton transfer mechanisms, and the ice surface and pre-melting[1]. Considering that the trial-and-error process of obtaining simulated AFM images that match the experimental image can be time-consuming, we are also exploring the application of machine learning to expedite structure determination with increased efficiency[7].
References:
[1]Jiani Hong, Ye Tian, Tiancheng Liang, et al. Nature (2024)
[2]Ye Tian, Yizhi Song, Y. Xia, Jiani Hong, Y. Huang, et al. Nature Nanotechnology 10, 1038. (2024).
[3]Y. Tian*, J. Hong*, D. Cao*, S. You*, Y. Song, et al. Science 377, 315-319 (2022).
[4]D. Cao, Y. Song, J. Peng, et al. Front Chem. 9, 745446 (2021)
[5]D. Cao, Y. Song, J. Peng, et al. Front Chem. 7, 626 (2019)
[6]J. Peng, D. Cao, Z. He, et al. Nature 557, 701-705 (2018).
[7]B. Tang*, Y. Song*, M. Qin*, et al. National Science Review. nwac282 (2022).
Amorphous solids and non-equilibruim phase transitions
Phase transitions are fundamental phenomena in statistical physics and thermodynamics. Almost four decades ago, a first-order-like non-equilibrium glass-glass transition (GGT) was discovered in water with two forms of amorphous ices were identified. Subsequently, GGT was observed in other materials, including water-like complex substances[1,2], colloids, particulate matter, polymers, liquid crystals, etc. However, statistical physics, thermodynamics, and condensed matter physics cannot describe the non-equilibrium phase transition of complex disordered systems. As a century problem in the 125th anniversary of Science, describing non-equilibrium phase transitions, such as glass transition and glass-glass transition, has been challenging due to the lack of well-established theories.
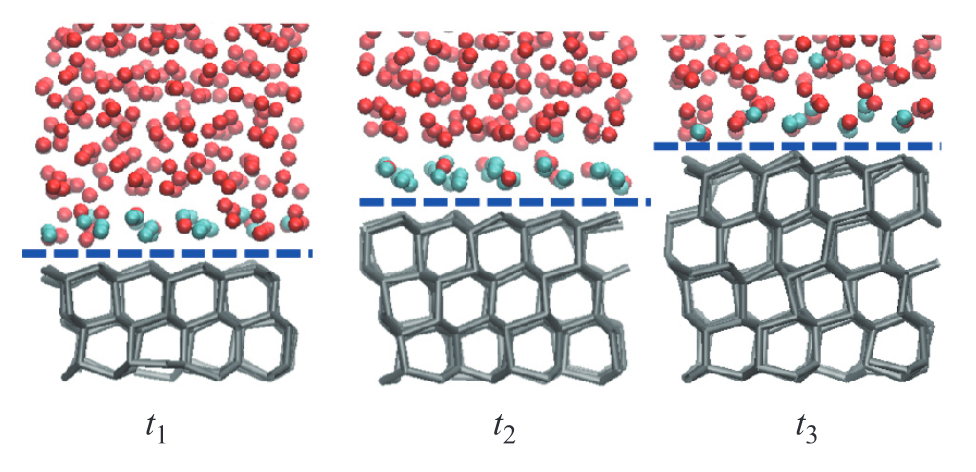
Although many challenges are faced, specific phenomena could still be focused on as interesting directions, one of them is the confined liquids in supercooled region. Liquids in confined geometries has obvious relevance in biology, geology, and other areas where the material properties are strongly dependent on the amount and behavior of liquids themselves in these types of materials, especially water[3]. Additionally, the crystallization of liquids confined at the nanoscale plays an important role in scientific and engineering applications, yet crystallization at the nanoscale is not well understood. Using molecular dynamics simulations, we study the crystallization of a confined liquid characterized by isotropic pair interactions with water-like properties, and find that increasing the liquid–surface interaction strength favors crystallization for the case of structureless surfaces, while it tends to suppress crystallization for the case of amorphous surfaces[4].
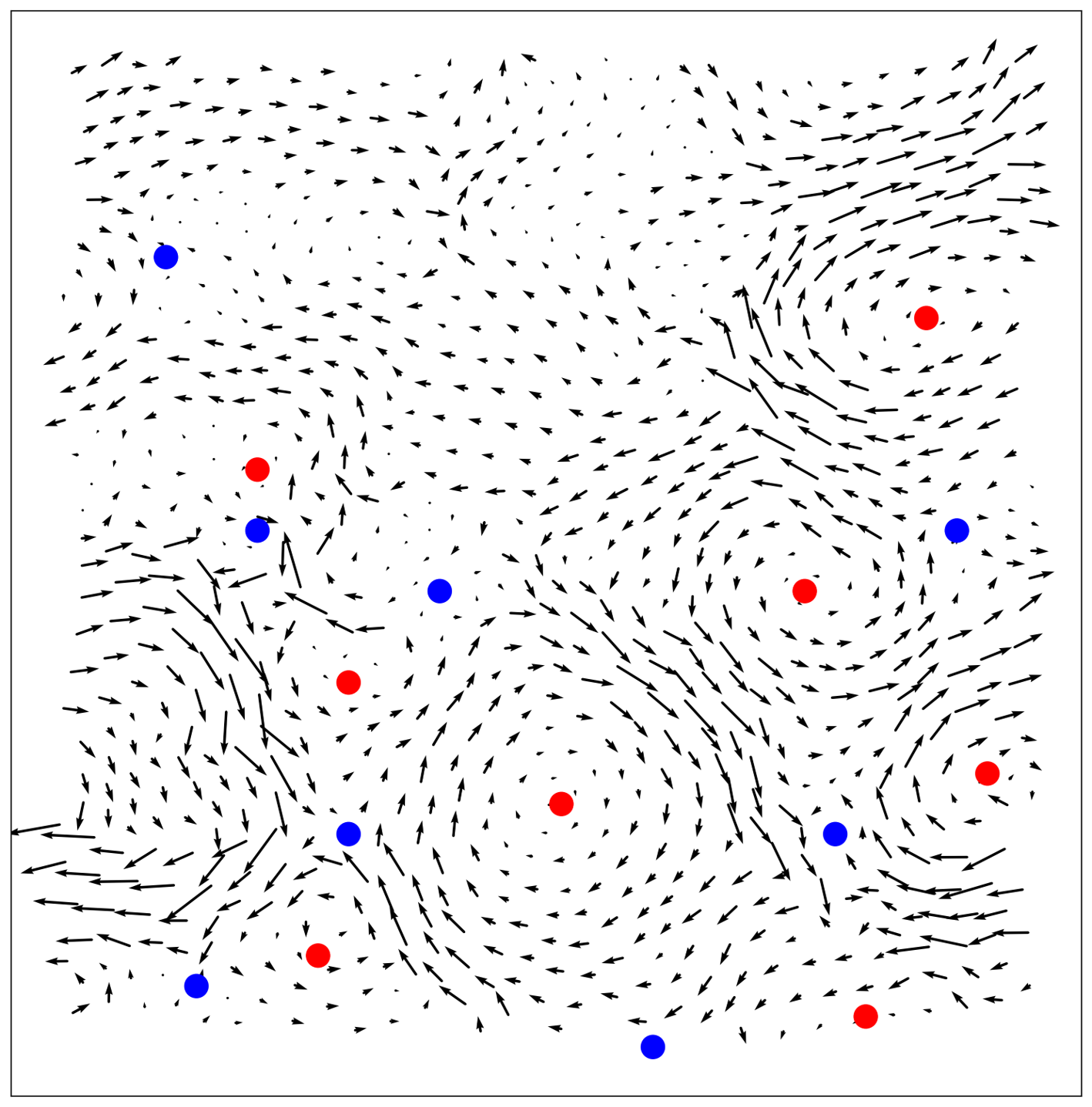
The behavior of amorphous solids is also attractive in this region. Glasses and other amorphous solids represent a class of materials that is both relatively commonplace and highly complex. Despite their familiarity, the fundamental physics underlying several common features of glasses is not yet well understood. While amorphous materials respond elastically to small applied strain, they undergo irreversible structural rearrangement for moderate deformation that is difficult to characterize and predict. Recently, significant effort has been put into forming structure-dynamics predictions for the failure behavior of disordered solids. These works attempt to identify structural precursors to plastic deformation, which occurs when glasses become unstable. We investigate the topological characteristics of the eigenvector field of the vibrational excitations of two-dimensional model glasses, and provide a link between the structure of glasses prior their deformation and the plastic events during deformation[5].
References:
[1]G. Sun, L. Xu, N. Giovambattista. Phys. Rev. Lett. 120, 035701 (2018)
[2]Y. Liu, G. Sun, L. Xu. The Journal of Chemical Physics, 154, 134503 (2021)
[3]S. Cerveny, F. Mallamace, J. Swenson, M. Vogel, and L. Xu. Chemical Reviews (2015)
[4]G. Sun, N. Giovambattista, E. G. Wang, and L. Xu*, et al. Soft Matter 9, 11374 (2013)
[5]Z. Wu, Y. Chen, W. Wang, W. Kob, L. Xu, Nat. Commun. 14, 2955(2023)